有向無(wú)環(huán)圖表達(dá)形式

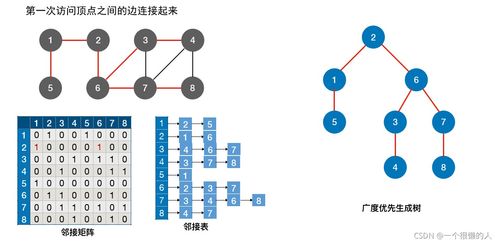
有向無(wú)環(huán)圖是一種重要的數(shù)據(jù)結(jié)構(gòu)，廣泛應(yīng)用于計(jì)算機(jī)科學(xué)和工程領(lǐng)域。其核心特點(diǎn)在于圖中不存在環(huán)路，即從任何一個(gè)頂點(diǎn)出發(fā)，沿著有向邊無(wú)法回到該頂點(diǎn)本身。這種結(jié)構(gòu)天然適合表示具有前后依賴(lài)關(guān)系或順序約束的場(chǎng)景。常見(jiàn)的表達(dá)形式包括鄰接矩陣和鄰接表。鄰接矩陣適用于稠密圖，可以快速判斷任意兩頂點(diǎn)間是否存在邊；而鄰接表則更節(jié)省空間，尤其適合表示稀疏的有向無(wú)環(huán)圖，它能清晰地列出每個(gè)頂點(diǎn)的所有后繼節(jié)點(diǎn)。

拓?fù)渑判颍豪砬逡蕾?lài)順序

拓?fù)渑判蚴轻槍?duì)有向無(wú)環(huán)圖的一種線性序列排序算法。它將圖中所有頂點(diǎn)排成一個(gè)線性序列，使得對(duì)于圖中的每一條有向邊(u, v)，在序列中頂點(diǎn)u都出現(xiàn)在頂點(diǎn)v之前。這實(shí)質(zhì)上是將圖的結(jié)構(gòu)關(guān)系轉(zhuǎn)化為一種可執(zhí)行的順序。

算法實(shí)現(xiàn)通常采用兩種方法：基于深度優(yōu)先搜索的后序遍歷逆序，或基于入度的Kahn算法。后者通過(guò)不斷移除入度為0的頂點(diǎn)并更新相關(guān)頂點(diǎn)的入度來(lái)實(shí)現(xiàn)排序。拓?fù)渑判蛟谌蝿?wù)調(diào)度、課程安排、編譯過(guò)程中的指令排序等方面有著重要應(yīng)用，它能有效解決任務(wù)間的依賴(lài)關(guān)系問(wèn)題。

關(guān)鍵路徑：優(yōu)化項(xiàng)目管理

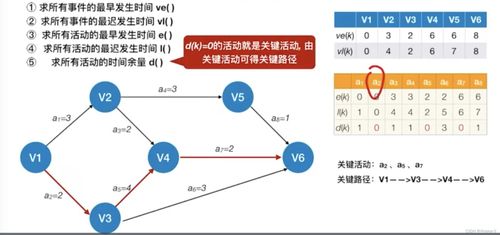
關(guān)鍵路徑方法基于有向無(wú)環(huán)圖，專(zhuān)門(mén)用于項(xiàng)目計(jì)劃管理。它通過(guò)分析項(xiàng)目中各項(xiàng)活動(dòng)的持續(xù)時(shí)間及其依賴(lài)關(guān)系，確定影響項(xiàng)目總工期的關(guān)鍵活動(dòng)和路徑。圖中頂點(diǎn)表示事件（如任務(wù)開(kāi)始或結(jié)束），邊表示活動(dòng)，邊的權(quán)重代表活動(dòng)持續(xù)時(shí)間。

關(guān)鍵路徑的求解涉及兩個(gè)核心計(jì)算：最早開(kāi)始時(shí)間和最晚開(kāi)始時(shí)間。通過(guò)正向計(jì)算各事件的最早發(fā)生時(shí)間，反向計(jì)算最晚發(fā)生時(shí)間，最終確定那些時(shí)間余量為零的活動(dòng)——這些活動(dòng)構(gòu)成了項(xiàng)目的關(guān)鍵路徑。任何關(guān)鍵活動(dòng)的延遲都會(huì)直接影響項(xiàng)目總工期，因此管理者需要特別關(guān)注這些環(huán)節(jié)的資源分配和進(jìn)度控制。

數(shù)據(jù)處理中的綜合應(yīng)用

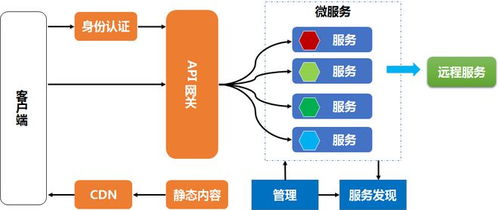
在實(shí)際數(shù)據(jù)處理中，有向無(wú)環(huán)圖及其相關(guān)算法形成了完整的問(wèn)題解決框架。從數(shù)據(jù)依賴(lài)分析到執(zhí)行計(jì)劃優(yōu)化，這一系列技術(shù)提供了系統(tǒng)化的解決方案。例如，在大數(shù)據(jù)處理框架如Apache Spark中，有向無(wú)環(huán)圖用于表示數(shù)據(jù)處理任務(wù)之間的依賴(lài)關(guān)系；在機(jī)器學(xué)習(xí)工作流中，它可用于管理特征工程、模型訓(xùn)練和評(píng)估的復(fù)雜管道。

將拓?fù)渑判蚺c關(guān)鍵路徑分析結(jié)合，不僅能確定任務(wù)執(zhí)行順序，還能識(shí)別影響整體處理時(shí)間的關(guān)鍵環(huán)節(jié)，從而實(shí)現(xiàn)資源的最優(yōu)配置和流程的高效執(zhí)行。這種基于圖的數(shù)據(jù)處理方法，為復(fù)雜系統(tǒng)的建模、分析和優(yōu)化提供了強(qiáng)有力的工具，在現(xiàn)代計(jì)算系統(tǒng)中發(fā)揮著不可替代的作用。